버블 정렬 Bubble Sort
비교정렬. 인접한 두 원소를 비교하여 정렬한다. 선택정렬과 유사
| 평균 시간복잡도 | 최선 시간복잡도 | 최악 시간복잡도 | 공간복잡도 | 안정 |
| O(n²) | O(n²) | O(n²) | O(1) | O |
장점: 구현 간단
단점: 최악과 최선의 시간복잡도가 같다. SWAP하는 과정이 데이터를 이동시키는것보다 복잡해서 잘 안쓰인다. 배열 길이가 길어질 수록 비효율적

선택 정렬 Selection Sort
제자리 비교 정렬. 특정 위치에 들어갈 원소(최소값 혹은 최대값)을 찾아서 특정 위치의 원소와 교환한다.
| 평균 시간복잡도 | 최선 시간복잡도 | 최악 시간복잡도 | 공간복잡도 | 안정 |
| O(n²) | O(n²) | O(n²) | O(1) | X |
장점: 구현 간단. 삽입정렬보다 안 좋다. 교환 연산은 최대 N번 이다.
단점: 최악과 최선의 시간복잡도가 같다. 배열 길이가 길어질 수록 비효율적

삽입 정렬 Insertion Sort
제자리 비교 정렬. 이미 정렬된 부분 배열과 특정 원소를 비교해서 삽입한다.
| 평균 시간복잡도 | 최선 시간복잡도 | 최악 시간복잡도 | 공간복잡도 | 안정 |
| O(n²) | O(n) | O(n²) | O(1) | O |
장점 : 구현 간단. 인접한 메모리와 비교해서 참조지역성이 좋다
단점: 시간복잡도, 배열 길이가 길어질 수록 비효율적. 원소의 이동이 많다.

변형에는 Shell Sort가 있다.
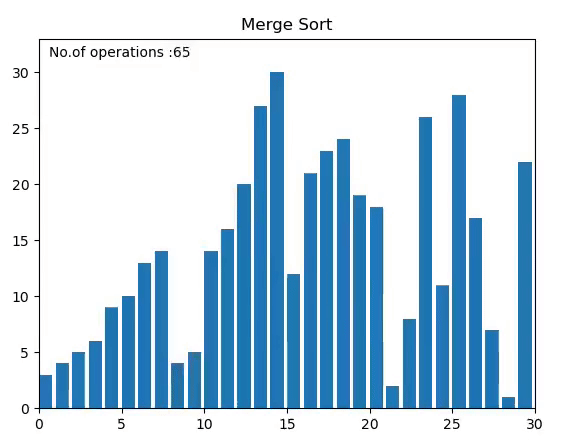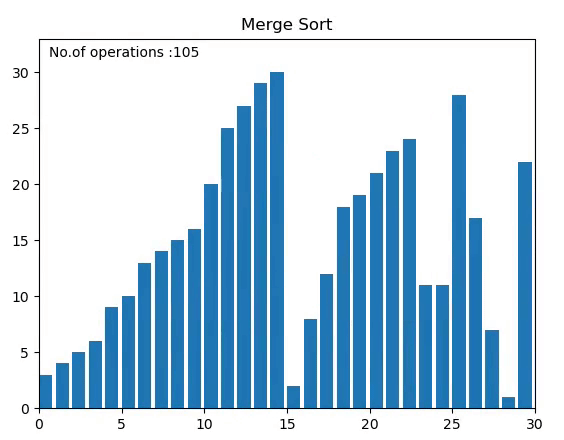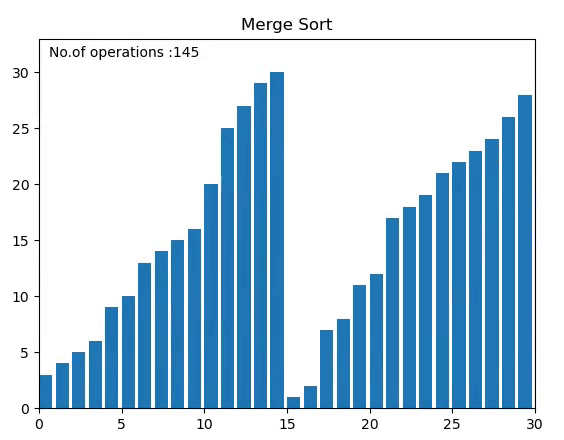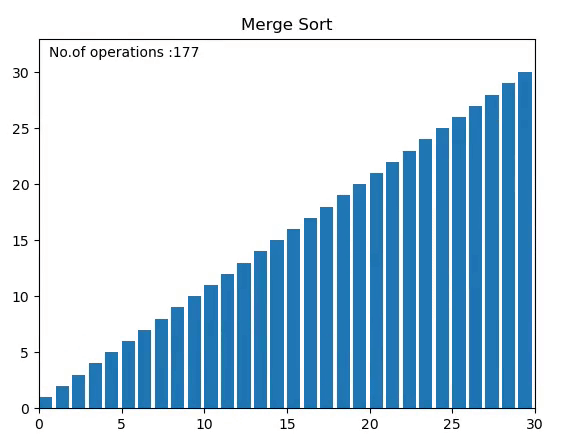
병합 정렬 Merge Sort
배열을 반으로 나눠서, 나눈 부분끼리 정렬하고 합치는 정렬
1. 분할: 배열을 반으로 나눈다.
2. 정복: 정렬한다. 원소의 수가 2개 이상이면 재귀적으로 병합정렬 한다.
3. 취합: 반으로 나눈걸 합친다.
| 평균 시간복잡도 | 최선 시간복잡도 | 최악 시간복잡도 | 공간복잡도 | 안정 |
| O(nlogn) | O(nlogn) | O(nlogn) | O(n) | O |
장점: 항상 동일한 시간복잡도
단점: 별도의 공간 요구
힙 정렬 Heap Sort
힙 자료구조를 이용한 정렬. 힙은 essentially complete binary tree 이다. 제자리 정렬.
1. 최대힙/최소힙 구조로 바꾼다.
2. 루트 노드와 가장 뒤쪽의 원소와 비교해서 교환한다.
3. 가장 뒤쪽의 원소는 정렬된 것으로 체크한다.
4. 1,2,3 과정을 반복한다
| 평균 시간복잡도 | 최선 시간복잡도 | 최악 시간복잡도 | 공간복잡도 | 안정 |
| O(nlogn) | O(n) | O(nlogn) | O(1) | X |
장점 : 추가공간 필요 없다. ( 배열로 이진 트리 구현 가능하기 때문에 )
단점 : 참조 지역성이 좋지 않다.
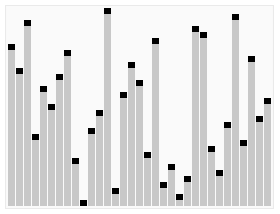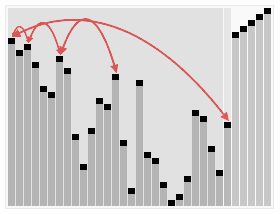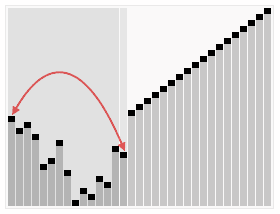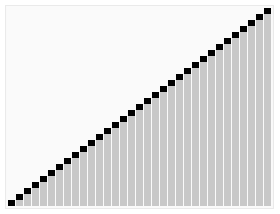
퀵 정렬 Quick Sort
배열을 둘로 나누고, 나눠진 배열을 재귀 호출로 정렬한다. 합병정렬과 다르게, 배열 분할 방식이 다르다.
( 제자리 정렬 아님!!!! )
1. 기준원소를 정하고, 기준원소기준으로 좌측은 작은 원소, 오른쪽은 큰 원소가 오게 한다..
2. 나눠진 배열을 따로 정렬한다. 즉, 재귀로 정렬
| 평균 시간복잡도 | 최선 시간복잡도 | 최악 시간복잡도 | 공간복잡도 | 안정 |
| O(nlogn) | O(nlogn) | O(n²) | O(logn) | X |
장점 : 참조지역성이 좋아서 다른 O(nlogn) 정렬에 비해 빠르다.
단점 : 최악의 경우, 즉 정렬된 경우 시간복잡도가 O(n²) 이다.
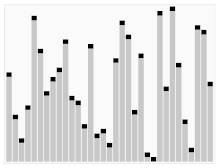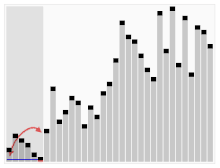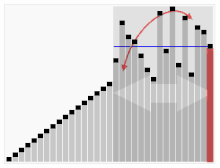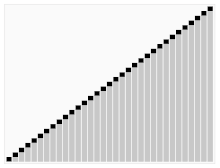
* 첫번째 원소를 기준 원소를 선택할 경우, 정렬된 경우에서 시간복잡도는 O(n²) 이다.
* 그래서 low, mid, high 값들 중 median을 피봇값으로 선택해서 부분배열 중 하나는 비어있지 않다고 보장할 수 있다.
* 최악의 공간복잡도는 O(n) 이다. 그러나, 재귀대신 반복문 사용해서 개선가능
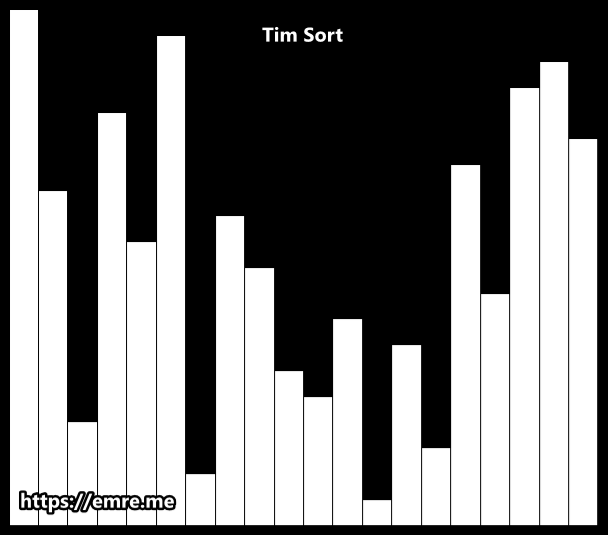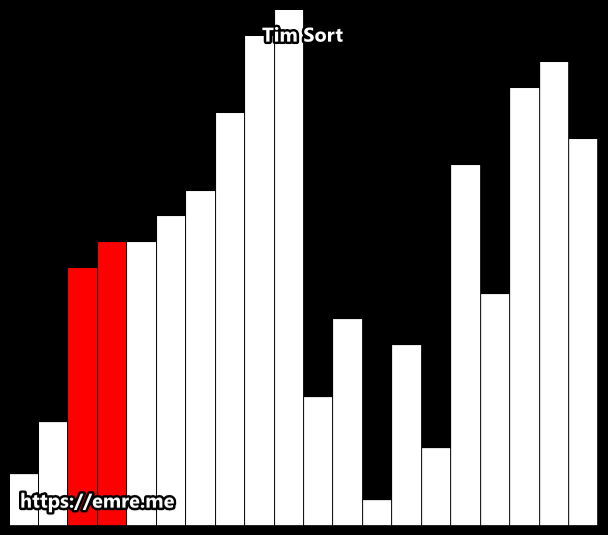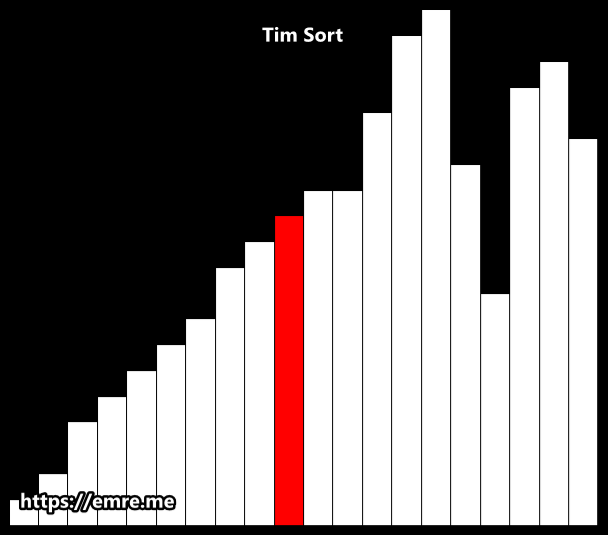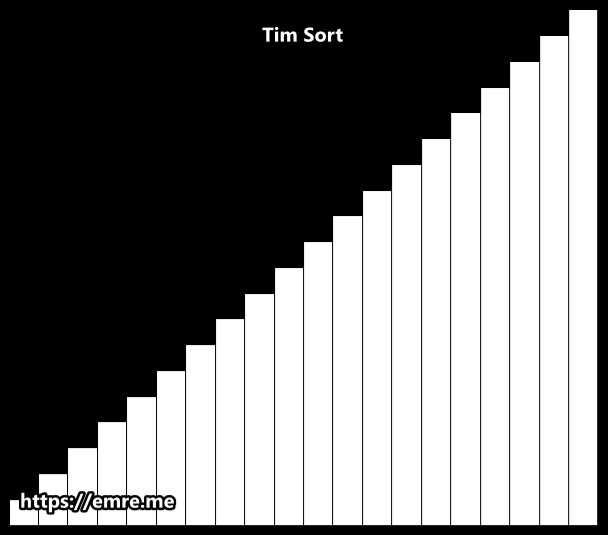
팀 정렬 Tim Sort
삽입정렬과 합병정렬을 결합한 알고리즘.
( 참조지역성 원리 만족하는 삽입정렬 사용 )
| 평균 시간복잡도 | 최선 시간복잡도 | 최악 시간복잡도 | 최악 공간복잡도 | 안정 |
| O(nlogn) | O(n) | O(nlogn) | O(n) | O |
1. Run
병합정렬과 달리 Run 단위로 짜른다 Run의 길이는 32 ~ 64 사이 값이다. 너무 작은 경우, 병합 많이 한다.
Run 단위 배열들은 inary Insertion Sort 를 이용해서 정렬한다.
2. Binary Insertion Sort
이분탐색 이용해서 삽입할 위치를 찾는다. 앞의 2개의 원소를 놓고 증가/감소를 결정한다.
앞의 2개의 원소를 ' 정렬 ' 되있다고 생각해서 삽입 위치를 찾는다.
검색에 O(logn), 데이터 삽입에 O(n) 이므로 O(nlogn) 만큼 걸린다.
이때, 이미 정렬된 경우 O(n) 정도 걸린다.
3. Merge
Run 단위로 머지를 하는데, 특정 조건에 만족해야 한다.
3-1 비슷한 길이끼리 merge 하는 것이 이득이기 때문에 stack 을 이용한다.
stack에 run 하나를 넣는데,
- stack[i] < stack[i+1]
- stack[i] + stack[i+1] < stack[i+2]
위 2조건을 만족해야 한다. 조건때문에 Run의 길이를 N이라고 하면 스택크기는 최대 logN이다.
두번째 조건은 피보나치와 유사하다.
만약 위 조건에 만족하지 않으면, 만족할 때 까지 run을 병합한다.
3-2 run들을 병합할 때는 작은 run만 복사를 한다.
그래서 기존 병합정렬처럼 오른쪽-> 왼쪽, 왼쪽 ->오른쪽 둘 다 할 수 있다.
작은 run만 복사했기 때문에 일반 병합정렬에 비해 메모리를 덜 쓴다.
* Galloping Search 고속 모드
Merge할 때 Run과 Run을 비교할 때, 원소의 크기를 1칸씩 비교하는 것이 아닌, 2^n 만큼 건너뛰면서 비교한다.
건너뛰다가, 선택되지 않는 부분 만났으면, 그 이전 지점과 현재 지점을 Binary Search해서 어디까지 Merge할지 결정한다.
처음부터 BinarySearch 안 쓰는 이유는, BestCase가 있을 수 도 있기 때문에 효율적인 Galloping Search를 쓴다.
처음 3개의 원소와 비교했을 때, 찾지 못했다면 Galloping Mode로 들어간다.
용어설명
안정정렬: 중복된 값이 존재할 때, 정렬 후에도 그 순서가 동일하다.
참조지역성: 정렬 알고리즘 시간을 계산할 때, 값을 읽어오는 위치에 따라 시간이 늘어날 수 있다.
참고
https://velog.io/@jeong-god/Tim-Sort%EB%8A%94-%EB%AC%B4%EC%97%87%EC%9D%B8%EA%B0%80
https://fluorescent-bay-98e.notion.site/SORT-952e4b5625fa4f4e967acde0aeecf9fa
https://d2.naver.com/helloworld/0315536
https://en.wikipedia.org/wiki/Timsort
'Algorithm' 카테고리의 다른 글
| 0/1 Knapsack Problem - DP (0) | 2022.02.04 |
|---|